Integer time series models for tuberculosis in Africa | Scientific Reports - Nature.com
Abstract
Tuberculosis, an airborne disease, is the deadliest human infectious disease caused by one single agent. The African region is among the most affected and most burdensome area in terms of tuberculosis cases. In this paper, we modeled the number of new cases of tuberculosis for 2000–2021 by integer time series. For each African country, we fitted twenty different models and selected the model that best fitted the data. The twenty models were mostly based on the number of new cases following either the Poisson or negative binomial distribution with the rate parameter allowed to vary linearly or quadratically with respect to year. The best fitted models were used to give predictions for 2022–2031.
Similar content being viewed by others

Infectious disease in an era of global change

Principal component analysis
The WHO estimates of excess mortality associated with the COVID-19 pandemic
Introduction
Tuberculosis (TB), an airborne disease, is the deadliest human infectious disease caused by one single agent, Mycobacterium tuberculosis (Mtb). The bacteria usually attacks the lungs, but it can also attack any part of the body such as the kidney, spine, and brain (CDC1). Fortunately, not everyone infected with TB bacteria becomes sick. Mtb is believed to have originated in East Africa around three million years ago but the first known description of TB was found in India and China as early as 3300 and 2300 years ago, respectively. While TB was a major cause of death in the 19th and early 20th centuries, the development of effective antibiotics in the mid-20th century led to a dramatic decline in the incidence of the malady (Dutta2).
TB continues to kill more than a million deaths per year in spite of a 47% drop in TB mortality rate since 1990. In 2021, 10.6 million people worldwide were diagnosed with TB with 1.6 million deaths, including 187,000 people with HIV, a major driver of TB (World Health Organization3).
Chakaya et al.4 believed that the COVID-19 pandemic worsened an already sub-optimal global TB response. According to the World Health Organization5, the disruption and reallocation of resources due to the COVID-19 pandemic has reversed years of global progress in reducing the number of people who die from TB with the estimated number of deaths in 2020 back to the level of 2017 leading to a reduction of only 9.2% instead of the targeted 35% reduction in the number of TB deaths between 2015 and 2020.
While TB can affect anyone irrespective of creed, the highest burden is in adult men, and those living in Africa and Asia. In this paper, we focus on African incidences. There are a number of reasons why TB is common in Africa. These include (i) poverty-which causes limited access to health care; (ii) HIV/AIDS-which weakens the immune system, making people more susceptible to TB. In Africa, about 25% of people living with HIV also have TB; (iii) weak health systems causing difficulties to diagnose and treat TB; (iv) a lack of awareness-which can lead to people not seeking treatment, inevitably causing the disease spread.
Figure 1 shows the estimated TB incidence rates in the world. Most of the countries having high TB incidence rates appear to be in Africa.
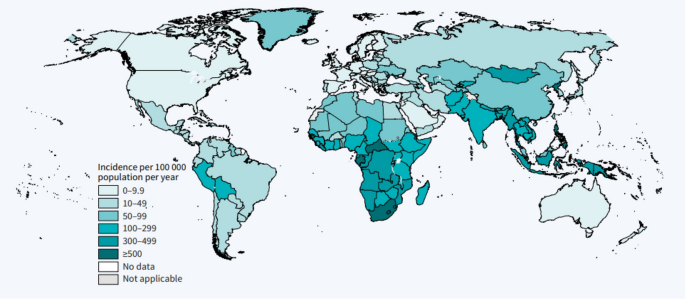
Estimated TB incidence rates, 2021. Source World Health Organization3 Global Tuberculosis Report.
According to Silva et al.6, fulfilling the UN Sustainable Development Goal (SDG) of ending the TB epidemic by 2030 is appearing more and more improbable. Silva et al.6 conducted a study estimating the economic impact of not meeting the target until 2045, including those due to excess deaths resulting from COVID-19-related disruptions to TB services for the period 2020–2050. They found that if the current rate of TB deaths continues, 31.8 million people will die from TB between 2020 and 2050, leading to an economic loss of $17.5 trillion. Meeting a 90 percent reduction in TB deaths by 2030 would save 23.8 million lives and $13.1 trillion. This would save $3.0 trillion in additional economic losses and likely spare the lives of 5.7 million additional individuals as compared to if the 90% reduction was to be met in 2045 instead. In short, meeting the SDG TB mortality target is essential to saving lives and preventing economic losses.
One way to model TB is through mathematical epidemiological models (see, for example, Ozcaglar et al.7). These models have the advantage of taking into account the dynamics of the disease and the researcher's understanding of the biological principles that drive the spread of the malady. For example, accounting for the slow spread of TB may result in more precise predictions for the long term. We are not so much interested in the dynamics of the disease as interest here is in the count of the number of people infected with the disease. Therefore, we use more of a statistical method.
Our modeling approach does not involve simulations, but instead fits a curve to the historical data. This way of modeling simply reflects the observed relationship between variables and attempts to forecast future results based on the past data (Dhlakama et al.8).
There has been research concerning the modeling of TB. Liu et al.9 developed a TB model incorporating seasonality based on data from China. They developed a compartmental model to describe TB seasonal incidence rate by incorporating periodic coefficients and discovered that there is a seasonal pattern of new TB cases, with those numbers peaking in late spring to early summer. Their research attributed the seasonal pattern to the Chinese Spring Festival, and/or to the more frequent viral infections like flu, which can lead to reactivation of the Mtb.
Using 462,214 pulmonary TB cases over a period of 10 years as training data, Liu et al.10 used two different approaches to predict the number of TB cases in Jiangsu Province, China. The first approach, autoregressive integrated moving average (ARIMA), is a statistical method that uses past data to predict future trends. The second approach, back-propagation neural network (BPNN), is a neural network method that uses statistical machine learning to learn from data. Both approaches were able to predict seasonality and trend of pulmonary TB in the Chinese population, but the BPNN approach was slightly more accurate.
Using multilevel modelling, Dhlakama et al.8 investigated factors that influence self-reported TB cases from 2008 to 2017. They discovered several variables that had a significant impact on TB such as marital status, gender, race, unemployment, other diseases, exercise patterns, smoking patterns, health consultation, asthma diagnosis, diabetes diagnosis, housing quality and household. The results were the same using both frequentist and Bayesian models even with informative priors.
In this paper, we model the prevalence of TB in Africa as calculated by incidence rate per 100,000 people. We model the distribution of the number of new cases of TB in a given year conditioned on the history of the number of cases up to that year. For each country, we fitted the incidence data using 20 models for integer time series and selected the best fitting model. Most of the twenty models were based on the number of new cases following either the Poisson or negative binomial distribution with the rate parameter allowed to vary linearly or quadratically with respect to year. Others were based on the number of new cases following either the Poisson or negative binomial distribution with the rate parameter allowed to depend on previous number of new cases. There are no papers modeling incidence rates of TB for all African countries.
The rest of the paper is structured as follows. "Data" section discusses the data, "Models" section discusses the models used to fit the data, "Results and discussion discusses the results and the paper is concluded in "Conclusion" section.
Data
According to the World Bank, TB incidence is the rate per 100,000 population of new and relapse TB cases that occur in a year. This number covers all types of TB such as other members of the Mtb complex and also cases in people living with HIV (World Bank11).
The countries in Africa.
The data are new cases of TB reported in \(2000, 2001, \ldots , 2021\) for the following African countries: Algeria, Angola, Benin, Botswana, Burkina Faso, Burundi, Cabo Verde, Cameroon, Central African Republic, Chad, Comoros, the Democratic Republic of Congo, Republic of Congo, Cote d'Ivoire, Djibouti, Egypt, Equatorial Guinea, Eritrea, Eswatini, Ethiopia, Gabon, the Gambia, Ghana, Guinea, Guinea-Bissau, Kenya, Lesotho, Liberia, Madagascar, Malawi, Mali, Mauritania, Mauritius, Morocco, Mozambique, Namibia, Niger, Nigeria, Rwanda, Sao Tome and Principe, Senegal, Seychelles, Sierra Leone, Somalia, South Africa, Sudan, Tanzania, Togo, Tunisia, Uganda, Zambia and Zimbabwe, see Fig. 2. The data were obtained from https://data.worldbank.org/indicator/SH.TBS.INCD. We were not able to obtain the data for Libya, South Sudan or Western Sahara.
Models
Let \(Z_t\) denote the number of new cases of TB reported in year t, \(t = 2000, 2001, \ldots , 2021\). Let \(\mathcal{F}_t\) denote the history of the number of new cases up to and including year t. For each of the fifty two countries, the following models were fitted
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Poisson \(\left( \beta _0 \right)\), referred to as the identity Poisson model;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Poisson \(\left( \exp \left( \beta _0 \right) \right)\), referred to as the log Poisson model;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Negative Binomial \(\left( \beta _0, \phi \right)\), referred to as the identity negative binomial model;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Negative Binomial \(\left( \exp \left( \beta _0 \right) , \phi \right)\), referred to as the log negative binomial model;
-
\(Z_t \mid \mathcal{F}_{t - 2} \sim\) Poisson \(\left( \beta _0 + \beta _1 Z_{t - 1} \right)\), referred to as the identity Poisson model regressed on the previous observation;
-
\(Z_t \mid \mathcal{F}_{t - 2} \sim\) Poisson \(\left( \exp \left( \beta _0 + \beta _1 Z_{t - 1} \right) \right)\), referred to as the log Poisson model regressed on the previous observation;
-
\(Z_t \mid \mathcal{F}_{t - 2} \sim\) Negative Binomial \(\left( \beta _0 + \beta _1 Z_{t - 1}, \phi \right)\), referred to as the identity negative binomial model regressed on the previous observation;
-
\(Z_t \mid \mathcal{F}_{t - 2} \sim\) Negative Binomial \(\left( \exp \left( \beta _0 + \beta _1 Z_{t - 1} \right) , \phi \right)\), referred to as the log negative binomial model regressed on the previous observation;
-
\(Z_t \mid \mathcal{F}_{t - 3} \sim\) Poisson \(\left( \beta _0 + \beta _1 Z_{t - 1} + \beta _2 Z_{t - 2} \right)\), referred to as the identity Poisson model regressed on the two previous observations;
-
\(Z_t \mid \mathcal{F}_{t - 3} \sim\) Poisson \(\left( \exp \left( \beta _0 + \beta _1 Z_{t - 1} + \beta _2 Z_{t - 2} \right) \right)\), referred to as the log Poisson model regressed on the two previous observations;
-
\(Z_t \mid \mathcal{F}_{t - 3} \sim\) Negative Binomial \(\left( \beta _0 + \beta _1 Z_{t - 1} + \beta _2 Z_{t - 2}, \phi \right)\), referred to as the identity negative binomial model regressed on the two previous observations;
-
\(Z_t \mid \mathcal{F}_{t - 3} \sim\) Negative Binomial \(\left( \exp \left( \beta _0 + \beta _1 Z_{t - 1} + \beta _2 Z_{t - 2} \right) , \phi \right)\), referred to as the log negative binomial model regressed on the two previous observations;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Poisson \(\left( \beta _0 + \beta _1 t \right)\), referred to as the identity Poisson model regressed linearly with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Poisson \(\left( \exp \left( \beta _0 + \beta _1 t \right) \right)\), referred to as the log Poisson model regressed linearly with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Negative Binomial \(\left( \beta _0 + \beta _1 t, \phi \right)\), referred to as the identity negative binomial model regressed linearly with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Negative Binomial \(\left( \exp \left( \beta _0 + \beta _1 t \right) , \phi \right)\), referred to as the log negative binomial model regressed linearly with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Poisson \(\left( \beta _0 + \beta _1 t + \beta _2 t^2 \right)\), referred to as the identity Poisson model regressed quadratically with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Poisson \(\left( \exp \left( \beta _0 + \beta _1 t + \beta _2 t^2 \right) \right)\), referred to as the log Poisson model regressed quadratically with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Negative Binomial \(\left( \beta _0 + \beta _1 t + \beta _2 t^2, \phi \right)\), referred to as the identity negative binomial model regressed quadratically with respect to year;
-
\(Z_t \mid \mathcal{F}_{t - 1} \sim\) Negative Binomial \(\left( \exp \left( \beta _0 + \beta _1 t + \beta _2 t^2 \right) , \phi \right)\), referred to as the log negative binomial model regressed quadratically with respect to year,
where \(\beta _0\), \(\beta _1\) and \(\beta _2\) are the regression coefficients. These models are due to Fokianos et al.12, Fokianos and Tjostheim13, Fokianos and Fried14 and Christou and Fokianos15,16. The models due to Christou and Fokianos15 are based on the negative binomial distribution. The models due to the others are based on the Poisson distribution. Both Poisson and negative binomial distributions are commonly implemented when dealing with count data.
The stated models were fitted by the method of maximum likelihood. That is, by maximizing
and
respectively, with respect to \(\beta _0\), \(\beta _1\), \(\beta _2\) and \(\phi\). We shall denote their maximum likelihood estimates by \(\widehat{\beta _0}\), \(\widehat{\beta _1}\), \(\widehat{\beta _2}\) and \({\widehat{\phi }}\), respectively. The likelihood functions were maximized using the command tsglm in the R package tscount (Liboschik et al.17; R Development Core Team18).
For each of the fitted models, we computed the Akaike Information Criterion (AIC) due to Akaike19, Bayesian Information Criterion (BIC) due to Schwarz20 and associated p-values of the Kolmogorov–Smirnov test (Kolmogorov8; Smirnov21) obtained by re-sampling. The values of AIC were computed as
and
The values of BIC were computed as
and
The best fitting model for each country was determined by values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test. The parameter estimates, 95% confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 1 when the best fitted model was the identity Poisson model. The parameter estimates, 95% confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 2 when the best fitted model was the log Poisson model. The parameter estimates, 95% confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov-Smirnov test are given in Table 3 when the best fitted model was the log Poisson model regressed linearly versus year. The parameter estimates, 95 percent confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 4 when the best fitted model was the log Poisson model regressed on the previous observation. The parameter estimates, 95 percent confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 5 when the best fitted model was the identity Poisson model regressed on the previous observation. The parameter estimates, 95% confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 6 when the best fitted model was the log negative binomial model regressed on the two previous observations. The parameter estimates, 95 percent confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 7 when the best fitted model was the log negative binomial model regressed linearly versus year. The parameter estimates, 95 percent confidence intervals and values of the AIC, BIC and p-values of the Kolmogorov–Smirnov test are given in Table 8 when the best fitted model was the log negative binomial model regressed on the previous observation.
Results and discussion
Models based on the negative binomial distribution gave the better fit for Sao Tome and Principe, Eritrea, Seychelles, Tanzania, Cabo Verde, Djibouti, Eswatini, Kenya, Lesotho, Malawi, Namibia, South Africa and Zimbabwe. Models based on Poisson distribution gave the better fit for Chad, Comoros, the Democratic Republic of Congo, Mauritius, Morocco, Nigeria, the Central African Republic, Benin, Botswana, Burkina Faso, Burundi, Cameroon, Cote d'Ivoire, Egypt, Equatorial Guinea, Ethiopia, Ghana, Guinea, Liberia, Madagascar, Mali, Mauritania, Niger, Senegal, Sudan, the Gambia, Uganda, Zambia, Gabon, Guinea-Bissau, Mozambique, the Republic of Congo, Rwanda, Sierra Leone, Somalia, Tunisia, Angola, Algeria and Togo.
In the following countries, the newly reported cases of TB exhibits a decreasing trend over 2000 to 2021: Benin, Botswana, Burkina Faso, Burundi, Cameroon, Cote d'Ivoire, Egypt, Ethiopia, Ghana, Guinea, Madagascar, Mali, Mauritania, Niger, Senegal, Sudan, The Gambia, Uganda, Zambia, Eritrea, Seychelles and Tanzania. The decreasing trend appears sharpest for Botswana and shallowest for the Gambia. Equatorial Guinea and Liberia exhibit positive trends in the newly reported cases of TB over 2000 to 2021. Equatorial Guinea has the sharper positive trend.
The number of new cases immediately preceding has a positive impact on the rate of new cases for Gabon, Guinea-Bissau, Mozambique, the Republic of Congo, Rwanda, Sierra Leone, Somalia, Tunisia, Angola, Algeria, Togo, Cabo Verde, Djibouti, Eswatini, Kenya, Lesotho, Malawi, Namibia, South Africa, Zimbabwe, and Sao Tome and Principe. The second to the previous number of new cases has a negative impact on the rate of new cases for Sao Tome and Principe.
Figures 3, 4, 5, 6, 7, 8, 9, 10 and 11 plot the predicted new number of cases of TB for the period 2022 to 2031. Also plotted in these figures are the median of the new number of cases and 95% confidence intervals of the new number of cases. For the identity Poisson model, log Poisson model, log Poisson model regressed linearly versus year, identity Poisson model regressed on the previous observation, log Poisson model regressed on the previous observation, log negative binomial model regressed linearly versus year, log negative binomial model regressed on the previous observation and the log negative binomial model regressed on the two previous observations, the predicted new number of cases, say P(t), was estimated by \(\widehat{\beta _0}\), \(\exp \left( \widehat{\beta _0} \right)\), \(\exp \left( \widehat{\beta _0} + \widehat{\beta _1} t \right)\), \(\widehat{\beta _0} + \widehat{\beta _1} Z_{t - 1}\), \(\exp \left( \widehat{\beta _0} + \widehat{\beta _1} Z_{t - 1} \right)\), \({\widehat{\phi }} \left( 1 - {\widehat{\phi }} \right) ^{-1} \exp \left( \widehat{\beta _0} + \widehat{\beta _1} t \right)\), \({\widehat{\phi }} \left( 1 - {\widehat{\phi }} ...
Comments
Post a Comment